Regresi Linier dengan Gradient Descent

Ketika pertama kali belajar regresi linier, sebagian besar dari kita langsung dikenalkan dengan fungsi lm() di R. Cukup satu baris kode, dan model pun langsung jadi. Tapi pernahkah Anda bertanya-tanya, bagaimana sebenarnya model itu bekerja? Apa yang terjadi di balik layar ketika fungsi itu dijalankan?

Salah satu cara paling umum untuk “mengajarkan” model menemukan hubungan terbaik antara variabel adalah melalui metode yang disebut gradient descent. Metode ini banyak digunakan, terutama dalam pembelajaran mesin (machine learning), karena fleksibel dan mampu menangani data dalam skala besar.

Di artikel ini, saya ingin mengajak Anda untuk melihat regresi linier dari sudut pandang yang berbeda — bukan dengan menggunakan fungsi otomatis, tapi dengan menghitungnya sendiri menggunakan algoritma gradient descent di R. Tujuannya sederhana: memahami logika dasar di balik proses pembelajaran model dengan cara yang intuitif dan praktis.

Tutorial ini merupakan pengantar sederhana untuk menggunakan algoritma gradient descent dalam memperkirakan parameter (kemiringan dan intersep) pada regresi linier standar, sebagai alternatif dari regresi ordinary least squares (OLS) yang menggunakan pendekatan maximum likelihood.

1 Ordinary Least Square Regression

Sebagai langkah awal, saya akan mensimulasikan data untuk melakukan regresi OLS standar dengan pendekatan maximum likelihood melalui perhitungan jumlah kuadrat (sums of squares). Setelah itu dijelaskan, saya akan mendemonstrasikan bagaimana gradient descent dapat digunakan sebagai pengganti, serta bagaimana cara menafsirkan hasilnya.

2 Data Simulasi

set.seed(123)

x <- runif(1000, -5, 5)
y <- x + rnorm(1000) + 3

3 Fit a linear model

lm <- lm( y ~ x ) 
mod <- print(lm)
#> 
#> Call:
#> lm(formula = y ~ x)
#> 
#> Coefficients:
#> (Intercept)            x  
#>      3.0118       0.9942

mod
#> 
#> Call:
#> lm(formula = y ~ x)
#> 
#> Coefficients:
#> (Intercept)            x  
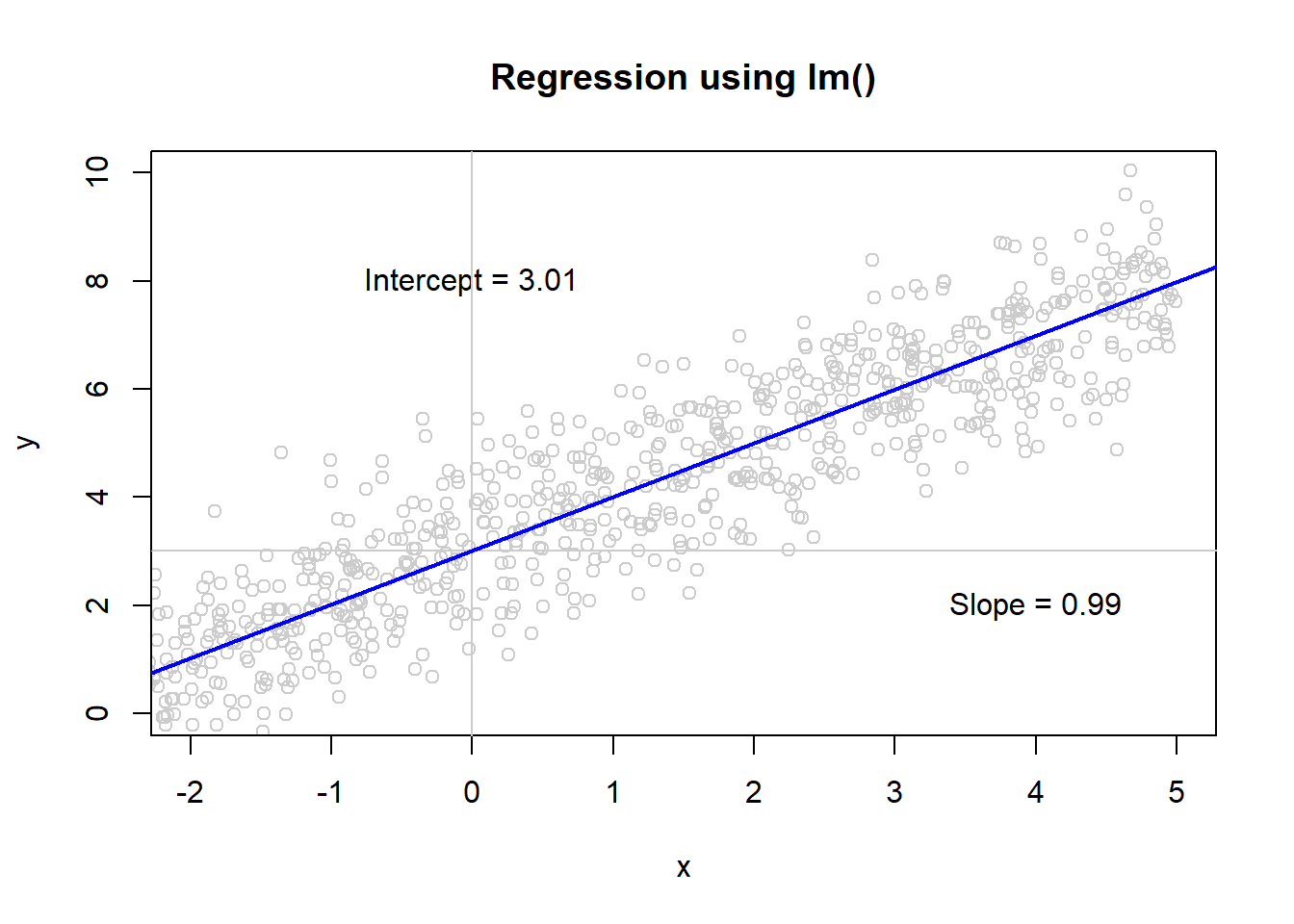
#>      3.0118       0.9942

4 Plot Data

plot(x,y, col = "grey80", main='Regression using lm()', xlim = c(-2, 5), ylim = c(0,10)); 
text(0, 8, paste("Intercept = ", round(mod$coefficients[1], 2), sep = ""));
text(4, 2, paste("Slope = ", round(mod$coefficients[2], 2), sep = ""));
abline(v = 0, col = "grey80"); 
abline(h = mod$coefficients[1], col = "grey80") 
abline(a = mod$coefficients[1], b = mod$coefficients[2], col='blue', lwd=2)

5 Gradient Descent

Untuk menilai seberapa baik suatu pasangan parameter (kemiringan dan intersep) dalam memodelkan data, kita akan menggunakan fungsi biaya error kuadrat (squared error cost function). Fungsi ini digunakan untuk menghitung tingkat kesalahan antara prediksi model dengan nilai sebenarnya, sehingga kita bisa mengetahui seberapa “tepat” tebakan kita terhadap nilai parameter tersebut.

cost <- function(X, y, theta) {
  sum( (X %*% theta - y)^2 ) / (2*length(y))
}

Kita juga perlu menetapkan dua parameter tambahan, yaitu learning rate dan batas jumlah iterasi. Learning rate mengatur seberapa besar langkah yang diambil saat memperbarui parameter, sedangkan batas iterasi menentukan berapa kali proses pembaruan tersebut dilakukan.

alpha <- 0.01
num_iters <- 1000

# keep history
cost_history <- double(num_iters)
theta_history <- list(num_iters)

# initialize coefficients
theta <- matrix(c(0,0), nrow=2)

# add a column of 1's for the intercept coefficient
X <- cbind(1, matrix(x))

# gradient descent
for (i in 1:num_iters) {
  error <- (X %*% theta - y)
  delta <- t(X) %*% error / length(y)
  theta <- theta - alpha * delta
  cost_history[i] <- cost(X, y, theta)
  theta_history[[i]] <- theta
}

print(theta)
#>           [,1]
#> [1,] 3.0116439
#> [2,] 0.9941657

6 Visualisasi Data dan Proses Konvergensi Model

iters <- c((1:31)^2, 1000)
cols <- rev(terrain.colors(num_iters))
library(gifski)
png("frame%03d.png")
par(ask = FALSE)

for (i in iters) {
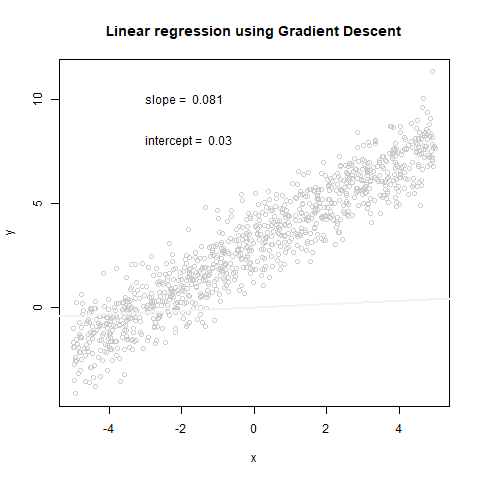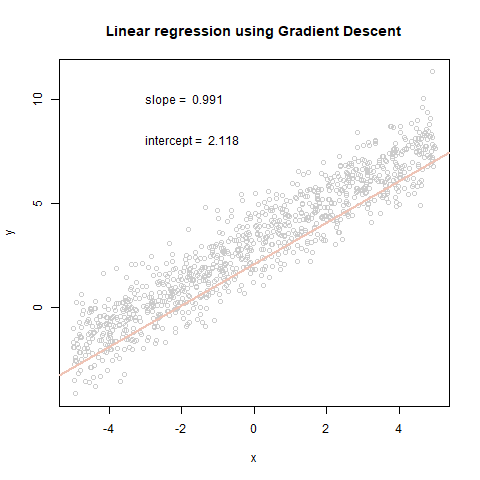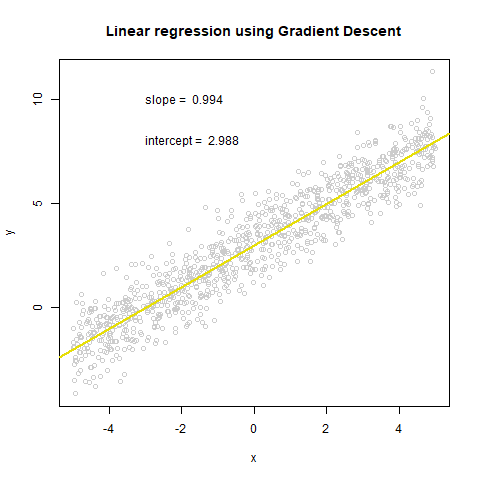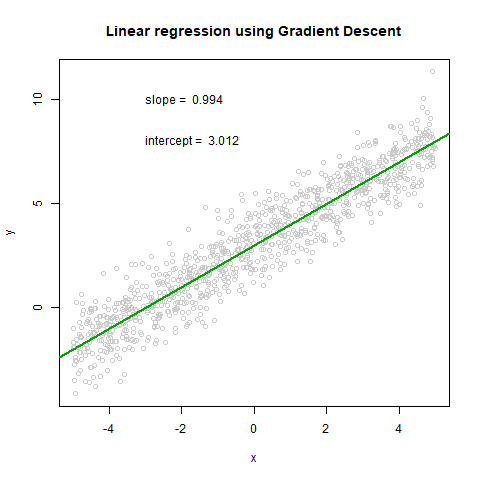
  plot(x,y, col="grey80", main='Linear regression using Gradient Descent')
  text(x = -3, y = 10, paste("slope = ", round(theta_history[[i]][2], 3), sep = " "), adj = 0)
  text(x = -3, y = 8, paste("intercept = ", round(theta_history[[i]][1], 3), sep = " "), adj = 0)
  abline(coef=theta_history[[i]], col=cols[i], lwd = 2)
}

dev.off()
#> png 
#>   2

## png 
##   2

png_files <- sprintf("frame%03d.png", 1:32)
gif_file <- gifski(png_files, delay = 0.1)
unlink(png_files)
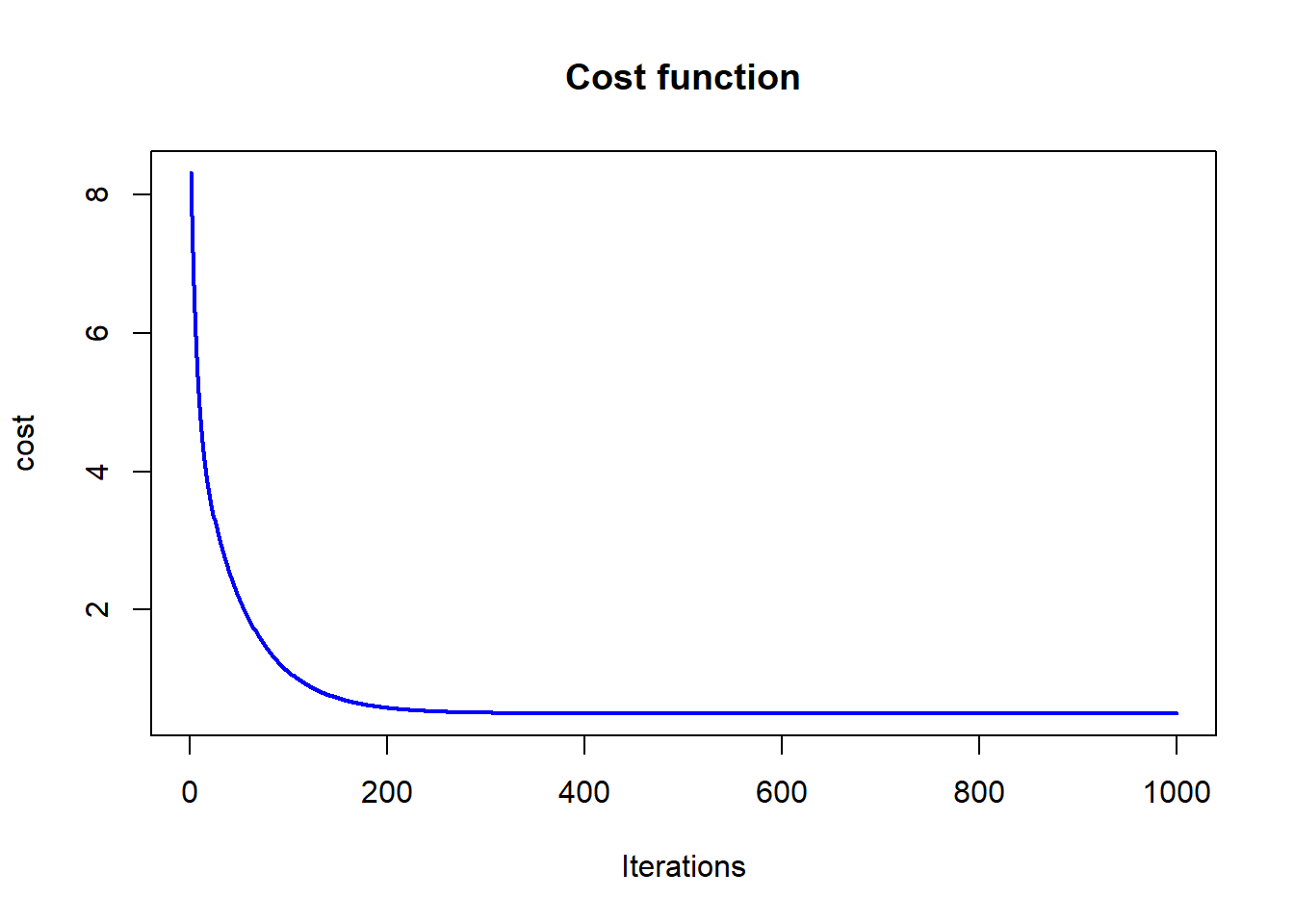
utils::browseURL(gif_file)

plot(cost_history, type='line', col='blue', lwd=2, main='Cost function', ylab='cost', xlab='Iterations')